Inhaltsverzeichnis:
- 1 Kirchhoffsche Gesetze für Ströme und Spannungen
- 2 Ohmsches und Kirchhoffsches Gesetz
- 3 Kirchhoffsches Gesetz für die Verteilung von Strömen in elektrischen Stromkreisen
- 4 Kirchhoffs Stromgesetz - physikalischer Sinn
- 5 Kirchhoffsches Gesetz für die Verteilung der Spannungen an den Elementen eines elektrischen Stromkreises
- 6 Kirchhoffs Spannungsgesetz - physikalischer Sinn
Die Gesetze der Physik ermöglichen es uns, die meisten Phänomene um uns herum besser zu verstehen – dies gilt auch für den Stromfluss.
Kirchhoffsche Gesetze für Ströme und Spannungen
In diesem Artikel stellen wir die theoretischen Grundlagen der Kirchhoff’schen Gesetze für Ströme und Spannungen in elektrischen Schaltungen vor und zeigen, wie sie in der Praxis funktionieren.
Ohmsches und Kirchhoffsches Gesetz
Um verschiedene physikalische Phänomene zu beschreiben, sei es in der Natur oder in künstlich geschaffenen Systemen, ist es notwendig, geeignete mathematische Werkzeuge zu verwenden. Dies gilt auch für die Beschreibung von Phänomenen, die in elektrischen Schaltkreisen auftreten. Neben dem Ohm’schen Gesetz sind die grundlegenden Werkzeuge für die mathematische Beschreibung elektrischer Schaltungen die Kirchhoff’schen Gesetze, die die Verteilung der Ströme in einem Knotenpunkt und die Verteilung der Spannungen auf den Elementen, die die Maschen der Schaltungen bilden, beschreiben. Die Kirchhoff’schen Gesetze können wie das Ohm’sche Gesetz sowohl auf elektronische Miniaturschaltungen als auch auf elektrische Stromkreise angewendet werden, die den für die Versorgung von Haushalten, Fabriken und anderen Einrichtungen benötigten Strom transportieren.
Kirchhoffsches Gesetz für die Verteilung von Strömen in elektrischen Stromkreisen
Wir verwenden das Kirchhoffsche Stromgesetz (abgekürzt PPK oder KCL), wenn wir die Ströme in Bezug auf den Knotenpunkt eines Stromkreises bestimmen wollen, an dem diese Ströme zusammenfließen. Betrachten wir die in Abbildung 1 dargestellte Situation, die ein Beispiel für einen aus Leitern mit Strömen gebildeten Knotenpunkt zeigt:

Wir können sehen, dass unser Knoten fünf Leitungen mit Strömen verbindet, aber diese Ströme haben unterschiedliche Flussrichtungen. Die Ströme I1, I2, und I3 sind Ströme, die in den Knoten fließen, und die Ströme I4 und I5 fließen aus demselben Knoten heraus. Ausgehend von den markierten Richtungen der Ströme können wir die Bilanzgleichungen für diese Ströme aufstellen:
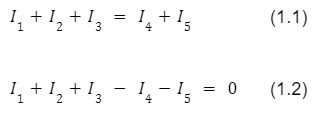
Aus den obigen Gleichungen folgt eine Schlussfolgerung, die als Kirchhoffsches Stromgesetz bezeichnet wird. Unter Bezugnahme auf Gleichung (1.1) besagt es, dass die algebraische Summe der Ströme, die in einen Knoten einfließen, gleich der Summe der Ströme ist, die aus demselben Knoten fließen. Gleichung (1.2) hingegen ist eine Umformung von Gleichung (1.1), aus der hervorgeht, dass die algebraische Summe der Ströme, die in einen Knoten hinein- und aus einem Knoten herausfließen, gleich Null ist.
Kirchhoffs Stromgesetz - physikalischer Sinn
Wenn wir uns den Stromfluss in einem Stromkreisknoten genauer ansehen, können wir auch die physikalische Bedeutung des Kirchhoffschen Stromgesetzes erkennen. Dieses besagt, dass die Anzahl der Elektronen, die pro Zeiteinheit in einen Knoten fließen, gleich der Anzahl der Elektronen ist, die aus dem Knoten fließen. Das bedeutet auch, dass sich an einem Knotenpunkt des Stromkreises keine Elektronen ansammeln können, aber auch nicht in einer unbekannten Richtung aus dem Knotenpunkt herausfließen können.
Kirchhoffsches Gesetz für die Verteilung der Spannungen an den Elementen eines elektrischen Stromkreises
Das Kirchhoffsche Stromgesetz beschreibt das Gleichgewicht der Ströme in einem Knotenpunkt, indem es ihre jeweiligen Rückflüsse zum selben Knotenpunkt angibt, d. h. die ein- und ausgehenden Ströme. Nach einem ähnlichen Prinzip wird das Kirchhoff’sche Spannungsgesetz (abgekürzt NPK oder KVL) vorgestellt, das die Berechnung der Spannungsverteilung über den Elementen eines Stromkreises ermöglicht, wobei das Vorzeichen der Spannung davon abhängt, ob es sich um die Quellenspannung oder den Spannungsabfall über dem Widerstand (oder bei Wechselstromkreisen die Impedanz) der Last handelt. Betrachten wir nun ein Beispiel für einen Stromkreis, der aus einem Netz mit drei Knotenpunkten besteht (Abbildung 2):
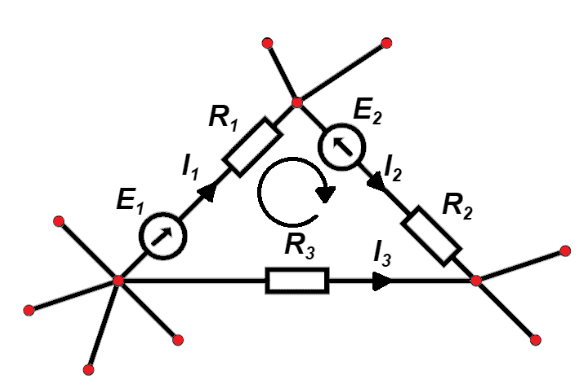
Zunächst müssen wir die konventionelle Richtung des Maschenstroms annehmen – in unserem Fall gehen wir von einer Orientierung im Uhrzeigersinn aus. Daher vergeben wir für Abzweigströme, die in Übereinstimmung mit der Ausrichtung der Masche fließen, ein “+”-Zeichen und für Ströme, die entgegengesetzt zur Ausrichtung dieser Masche fließen, ein “-” Zeichen. Andererseits nehmen wir bei der Beschreibung von Spannungen an Schaltungselementen für Spannungen, die dem fließenden Strom an einem bestimmten Element entgegengesetzt sind, das Vorzeichen “-” an, und wenn die Spannung entsprechend der Ausrichtung des Maschenstroms gerichtet ist, nehmen wir das Vorzeichen “+” an. Unter Bezugnahme auf die Standardform des Ohm’schen Gesetzes für stationäre Gleichstromkreise und auf die beschriebene Konvention zur Kennzeichnung von Strömen und Spannungen können wir die Spannungsbilanzgleichung unserer Schaltung (2.1) aufstellen:
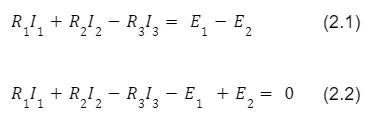
Aus Gleichung (2.1) ergibt sich das Kirchhoffsche Spannungsgesetz, das besagt, dass die algebraische Summe der Spannungsabfälle über dem Widerstand (oder bei Wechselstromkreisen der Impedanz) der Empfänger in einem Schaltkreisnetz gleich der Summe der Quellenspannungen in demselben Netz ist. Wird umgekehrt Gleichung (2.1) in Gleichung (2.2) umgewandelt, erhält man eine leicht abgewandelte Form des Kirchhoffschen Spannungsgesetzes, das besagt, dass die Summe der Spannungsabfälle über den Empfängern und den Quellenspannungen in einer Masche gleich Null ist.
Kirchhoffs Spannungsgesetz - physikalischer Sinn
Wie das Kirchhoffsche Stromgesetz ist auch das Kirchhoff’sche Spannungsgesetz physikalisch sinnvoll. Es drückt aus, dass wir, wenn wir uns entlang der Masche des Stromkreises durch Quellen elektromotorischer Kraft, an denen die Spannung steigt, und durch Empfänger, an denen die Spannung sinkt, bewegen, nach einem einzigen Kreislauf entlang der Masche zum Ausgangspunkt und zum gleichen Wert des elektrischen Potenzials zurückkehren. Dies bedeutet, dass die Masche des Stromkreises nicht gleichzeitig eine Spannungsquelle und eine Last sein kann, an der ein Spannungsabfall auftritt.
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!
Durchschnittliche Bewertung 5 / 5. Stimmenzahl: 5
Bisher keine Bewertungen! Sei der Erste, der diesen Beitrag bewertet.






















