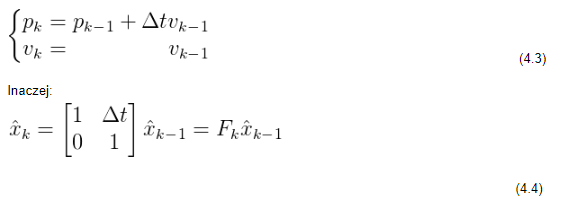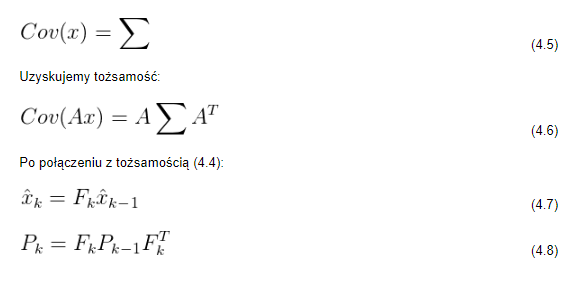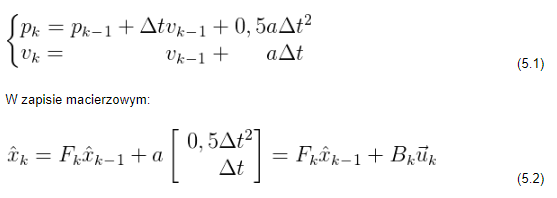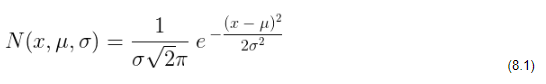Kalman-Filter – Theoretische Grundlage

Ein breites Spektrum technischer Wissenschaften benötigt geeignete mathematische Werkzeuge, um eine Vielzahl von Phänomenen zu beschreiben. Sowohl Automatisierung, Robotik, Steuerungstheorie und -systeme, Elektronik, Elektroakustik, digitale Signalverarbeitung und verwandte Bereiche stützen sich auf lineare Algebra, Operatorenkalkül, genetische Algorithmen, numerische Methoden sowie Fuzzy-Logik und andere Zweige der Mathematik. Neben den in den technischen Wissenschaften beliebten mathematischen Werkzeugen wie der Laplace-Transformation, der Z-Transformation oder der Finite-Elemente-Methode sticht vor allem ein Algorithmus hervor, der unter anderem die Weltraumforschung revolutioniert hat, nämlich der Kalman-Filter. Er ist eines der klassischen Schätzverfahren, das in Anwendungen wie der Signalverarbeitung, der Steuerung elektrischer Antriebe, autonomen Fahrzeugsteuerungssystemen und der Prozessorsteuerung in Computern eingesetzt wird. In der Fachliteratur wird der Kalman-Filter meist in spezifischen Anwendungsfällen wie autonomen Robotern oder linearen automatischen Steuerungssystemen mit Gauß-verteiltem Rauschen beschrieben, was es sehr schwierig macht, das Thema von der grundsätzlichen Seite her transparent darzustellen. Unser Artikel beschreibt den diskreten Kalman-Filter mit Hilfe der Vektor- und Matrizenrechnung und zeigt ein praktisches Beispiel für seine Anwendung.

Was ist ein Kalman-Filter?

Der Kalman-Filter ist ein spezieller Algorithmus, der in den frühen 1960er Jahren von Rudolf Emil Kalman (1930-2016), einem ungarisch-amerikanischen Elektroingenieur, entwickelt und vorgestellt wurde. Wir können den Kalman-Filter in jeder Anwendung einsetzen, bei der die Zuverlässigkeit der Informationen über die Parameter dynamischer Systeme eingeschränkt ist. Dann können wir auch vorhersagen, welche Ereignisse als nächstes eintreten könnten. Dies geschieht auf der Grundlage der bisher gesammelten Informationen. Dabei werden viele bedingte Faktoren berücksichtigt, die sich ändern und einen erheblichen Einfluss auf das Ergebnis des Automatisierungssystems haben können, in dem der Kalman-Filter eingesetzt wird. Dieser Algorithmus eignet sich hervorragend für dynamische Systeme, bei denen sich die Parameter ständig ändern und die keinen großen Speicherplatz benötigen, um ordnungsgemäß zu funktionieren, sondern nur den Zustand des Systems vor dem nächsten. Ein wichtiger Faktor, der dafür spricht, ist die hohe Geschwindigkeit des Algorithmus, wodurch er erfolgreich in Echtzeitanwendungen und eingebetteten Systemen eingesetzt werden kann.

Kalman-Filter – in welchen Anwendungen lohnt sich der Einsatz?

Bevor wir den Algorithmus erläutern, der das Prinzip des Kalman-Filters zeigt, werden wir ein Hardware-Beispiel für seine Anwendung verwenden, nämlich einen Roboter, der durch dicht bewaldete Gebiete navigieren kann. Er muss seine genaue Position kennen, damit das eingebaute Navigationssystem richtig funktioniert.

Wir können also sagen, dass unser Roboter durch eine Zustandsvariable xk, definiert ist, die durch einen Vektor mit zwei Komponenten – Position p und Geschwindigkeit v– definiert ist:

(3.1)

Der Zustand des Systems wird durch numerische Daten bestimmt, die seine Grundkonfiguration definieren, und dies können numerische Daten für beliebige Größen sein. In unserem Fall sind diese Größen Position und Geschwindigkeit, aber bei anderen Systemen kann es sich auch um die verbleibende Kraftstoffmenge im Tank des Autos, die Temperatur der Spitze im Kolben der Lötstation, den Strom im Erregerkreis des Synchrongenerators und viele andere Parameter handeln, die je nach Anwendung Verfolgungswerte erfordern. Der Roboter in dem hier vorgestellten Beispiel ist mit einem GPS-Navigationssystem ausgestattet, das in der Lage ist, seine Koordinaten mit einer Genauigkeit von zehn Metern zu bestimmen. Dies ist ein zufriedenstellendes Ergebnis, aber aufgrund der Variabilität der verschiedenen Parameter des Geländes, über das sich der Roboter bewegt, muss das eingebaute GPS-System noch genauer sein. Im schlimmsten Fall könnte der Roboter bei einer Koordinatengenauigkeit von zehn Metern sogar in einen Abgrund stürzen.

Um den Weg eines Roboters genau zu bestimmen, müssen die Parameter der einzelnen Signale, die seine Antriebseinheit steuern, bekannt sein. Dann “weiß” das GPS-System, dass der Roboter, wenn er sich mit einer quasi-geradlinigen Bewegung fortbewegt, sich im nächsten Schritt wahrscheinlich auf dieselbe Weise und in dieselbe Richtung weiterbewegen wird. Der Roboter erhält jedoch immer noch keine Informationen über Umgebungsfaktoren, die seine Bewegung beeinträchtigen können, z.B. Windböen, rutschiger Boden sowie Unebenheiten des Geländes und bisher nicht vorhergesehene Hindernisse auf der Straße (z.B. liegende Äste). Dann kann die Anzahl der Umdrehungen, die die Räder des Roboters auf der Straße machen, seine Bewegung falsch darstellen, was zu einer falschen Vorhersage des nächsten Schrittes führt, der die Bewegung des Roboters beschreibt.

Die GPS-Sensoren liefern indirekte Informationen über den Zustand des Systems (des Roboters), allerdings mit begrenzter Genauigkeit. Die GPS-Sensoren liefern indirekte Informationen über den Zustand des Systems (des Roboters), jedoch mit begrenzter Genauigkeit. Es scheint jedoch, dass die von den GPS-Sensoren empfangenen Daten im Schätzungsprozess verwendet werden können, um Koordinatenmessungen mit höherer Genauigkeit zu erhalten. Zu diesem Zweck hat sich unter anderem der als Kalman-Filter bekannte Algorithmus bewährt.

Kalman-Filter – der Anfang des Algorithmus

Um den Kalman-Filter-Algorithmus zu beginnen, schreiben wir die Zustandsvektor-Gleichung (3.1) in Matrixform:

(3.2)

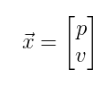
Wir kennen die aktuelle Position und Geschwindigkeit des Objekts nicht, denn es gibt eine endliche Menge, die den gesamten Bereich möglicher Kombinationen von Position und Geschwindigkeit abdeckt, die sich als mit der Realität übereinstimmend erweisen können, aber unter ihnen gibt es einige, die mehr oder weniger mit den tatsächlichen Werten übereinstimmen. Der Algorithmus des Kalman-Filters geht davon aus, dass beide Zustandsvariablen (in dem untersuchten Fall sind dies die Position und die Geschwindigkeit des Objekts) gemäß einer Gaußschen Verteilung (Normalverteilung) verteilt sind. Jede Variable hat einen Mittelwert, der in der Mitte der Zufallsverteilung liegt und auch der erwartete Wert ist, und eine Varianz, die die Messunsicherheit definiert. Auf den ersten Blick sind die Position und die Geschwindigkeit eines Objekts nicht miteinander verbunden, was bedeutet, dass die Information über den Zustand einer einzelnen Variablen (eine Komponente des Zustandsvektors) nicht ausreicht, um die andere Variable zu bestimmen. Tatsächlich sind die Position und die Geschwindigkeit eines Objekts miteinander verbunden, d.h. die Wahrscheinlichkeit, einen bestimmten Wert der Variable zu beobachten, die die Position eines Objekts bestimmt, hängt von seiner Geschwindigkeit ab.

Diese Situation kann z.B. auftreten, wenn Sie die vorherige Position eines Objekts kennen und versuchen, seine aktuelle Position zu bestimmen. Wenn die Geschwindigkeit des Objekts zu hoch ist, dann wird die nächste Positionsmessung des Objekts weiter entfernt sein. Bewegt sich das Objekt dagegen mit einer geringeren Geschwindigkeit, dann zeigt die Positionsmessung im Vergleich zur vorherigen Messung eine geringere Entfernung des Objekts an als bei einer höheren Geschwindigkeit. Die Beziehung zwischen der Position und der Geschwindigkeit eines Objekts ist bei der Verfolgung eines Objekts sehr wichtig, da sie wertvolle Informationen liefert – eine einzelne Parametermessung leitet die potenziellen Ergebnisse nachfolgender Messungen der gleichen Parameter. Dies ist der Hauptzweck des Kalman-Filter-Algorithmus – möglichst viele der durch Messungenauigkeiten belasteten Daten zu sammeln, um ein möglichst genaues Messergebnis zu erhalten. Die Beziehung zwischen den Zustandsvariablen wird durch die Kovarianzmatrix und jedes in ihr enthaltene Element definiert. Das Element definiert dann den Grad der Korrelation zwischen der i Zustandsvariablen und der j Zustandsvariablen, wobei die Kovarianzmatrix eine quadratische Matrix ist, d. h. die Anzahl ihrer Zeilen ist gleich der Anzahl ihrer Spalten.

Matrix-Notation

Um den Zustand eines Objekts zu modellieren, ist es hilfreich, die Matrixnotation mit Gaußscher Unschärfe zu verwenden – wir brauchen dann zwei Gleichungen, um den Zustand des Objekts für die K Messung_.xk zu bestimmen ist ein Vektor von Mittelwerten (skalar), die die erwarteten Werte sind, und P_k ist die Kovarianzmatrix.

Im vorliegenden Fall sind die Zustandsvariablen die Position und die Geschwindigkeit des Objekts, aber es sei darauf hingewiesen, dass der Zustand durch eine beliebige Anzahl von Variablen beschrieben werden kann, die beliebige Parameter darstellen. Es ist dann notwendig, die Werte der Variablen für den aktuellen Zustand (zum Zeitpunkt k-1) zu notieren, um mit der Vorhersage der Werte für den Zustand zum Zeitpunkt k fortfahren zu können. Es ist nicht bekannt, welcher Zustand die tatsächlichen Parameter des Objekts widerspiegelt, aber das ist für den Vorhersageprozess irrelevant. Die Vorhersagephase kann mit Hilfe des Vektors F_k visualisiert werden. Jeder Punkt, der sich im aktuellen Schritt im Zustandsraum befindet, wird in eine neue Region verschoben – die Region der vorhergesagten Werte, in die sich das System bewegt, wenn der vorhergehende Zustandsraum korrekt lokalisiert wurde. Um den vorhergesagten Zustandsraum zu finden, wenn Sie die aktuellen Werte der Zustandsvariablen kennen, die die Position und die Geschwindigkeit bestimmen, verwenden Sie ein System von Gleichungen:

Auf diese Weise erhalten wir eine Vorhersagematrix, die Informationen über den nächsten (nach k-1) Zustand (k) enthält. Es ist jedoch immer noch nicht klar, wie man die Kovarianzmatrix korrekt aktualisiert. Hier muss jeder Punkt, der in der Verteilung enthalten ist, mit der Matrix A multipliziert werden:

Einfluss von externen Faktoren

In diesem Stadium sind noch nicht alle Faktoren berücksichtigt. Dabei handelt es sich um Faktoren, die nicht direkt mit den Eigenschaften des untersuchten Systems zusammenhängen, sondern unabhängig davon auftreten, aber ebenfalls den Zustand des Systems beeinflussen können. Wenn es sich bei dem durch die Zustandsvariablen beschriebenen Objekt beispielsweise um eine elektrische Lokomotive handelt – wenn der Fahrer die Versorgungsspannung für die Motoren erhöht, z.B. durch Verringerung des magnetischen Flusses im Erregerkreis, beschleunigt die Lokomotive. Auch im beschriebenen Fall des Roboters kann das bordeigene Navigationssystem Probleme haben, ein Signal an das Steuersystem des Roboters zu übermitteln, um die Räder zu drehen oder anzuhalten, z.B. wenn die Gefahr besteht, dass der Roboter während der Fahrt vom Wind umgeweht wird. Wenn diese zusätzlichen Informationen über die äußeren Bedingungen bekannt sind, können sie mit Hilfe eines

_k-Vektors berücksichtigt werden, so dass die Korrektur in die Vorhersagematrix aufgenommen werden kann:

Wenn wir davon ausgehen, dass wir auf der Grundlage der Steuersignale (z.B. des Füllfaktors des Steuersignals für die Motordrehzahl) den erwarteten Wert der Beschleunigung a kennen, erhalten wir ein System von Gleichungen:

_k ist der Kontrollvektor – bei einfachen Systemen ohne äußere Einflüsse können diese Komponenten ignoriert werden. Was aber, wenn die vorhergesagte Lösung immer noch nicht genau genug ist?

Externe Unsicherheit

Der gesamte Vorhersageprozess geht nahtlos weiter, wenn der Zustand des Objekts auf allen berücksichtigten Faktoren basiert, einschließlich externer Faktoren, deren Auftreten nicht mit den Eigenschaften des Systems selbst zusammenhängt, die sie beeinflussen. Das ist so lange der Fall, wie wir die maximalen Parameter der externen Faktoren kennen, gegen die das System resistent sein wird. Was aber, wenn Faktoren auftreten, von denen wir nichts wissen? Drohnen (wie auch andere Flugzeuge) sind zum Beispiel Windböen ausgesetzt, die die Flugbahn stören und sogar eine Kollision mit einem nahe gelegenen Objekt (z. B. einem Baum) verursachen können. Ein Roboter mit Rädern kann während der Fahrt ausrutschen, so dass er trotz sich drehender Räder nicht mehr weiterfahren kann. Da diese Faktoren nicht berücksichtigt werden, kann der Algorithmus in der Vorhersagephase versagen, was sogar zu irreparablen Schäden am System führen kann.

Um die Wahrscheinlichkeit solcher höchst unerwünschten Effekte zu erhöhen, muss für jeden Vorhersageschritt eine zusätzliche Unsicherheit in die Berechnung einbezogen werden. Bei der originalen Schätzung wird dann die ursprüngliche Schätzung um einen Bereich von Zuständen erweitert. Die vorhergesagte Lösung x_k-1, wird in den Kovarianzbereich Q_k verschoben. Mit anderen Worten, man kann auch sagen, dass externe Faktoren, die eine Quelle zusätzlicher Unsicherheit sind, das Rauschen der Kovarianzmatrix Q_k bilden. Ein solcher Vorgang führt zu einer neuen Gaußschen Unschärfe, die eine andere Kovarianz in Bezug auf die ursprüngliche Gaußsche Unschärfe, aber denselben Erwartungswert der Zustandsvariablen hat. Anschließend erhält man eine erweiterte Kovarianzmatrix, indem man den Faktor Q_k einbezieht:

Mit anderen Worten: Der aktualisierte ‘beste’ erwartete Wert wird aus dem vorherigen erwarteten Wert unter Berücksichtigung der Auswirkungen der externen Bedingungen vorhergesagt. Auch die neu abgeleitete externe Unsicherheit ist das Ergebnis der Kombination der zuvor berechneten externen Unsicherheit mit einer erweiterten Unsicherheit aufgrund des Einflusses der externen Bedingungen. In diesem Stadium können wir die Daten von den Messsensoren weiterverarbeiten.

Annäherung an eine messbasierte Schätzung

Das zu prüfende System kann mit mehreren Messsensoren ausgestattet sein, die die notwendigen Informationen zur Bestimmung seines Zustands liefern. Unabhängig von den Stimulationen, auf die diese Sensoren reagieren, liefern sie die Informationen, die zur Bestimmung der Position und der Geschwindigkeit des Roboters erforderlich sind, so dass indirekte Messungen mit ihnen durchgeführt werden. Es ist wichtig zu beachten, dass es eine Abweichung zwischen den Einheiten und dem Maßstab der Anzeige und den Einheiten und dem Maßstab des verfolgten Zustands geben kann. Daher wird die Beschreibung der Sensoren durch eine H_k-Matrix modelliert. Die Verteilung der Sensormesswerte kann anhand der Gleichungen vorhergesagt werden:

Einer der größten Vorteile des Kalman-Filter-Algorithmus ist, dass er gegen die Ungenauigkeit der von den Sensoren vorgenommenen Messungen (aufgrund von Rauschen) immun ist. Sensoren können unzuverlässig sein, so dass jeder geschätzte Zustand des Systems das Ergebnis einer Reihe von Parametern sein kann, die von den Sensoren abgelesen werden. Der Kalman-Filter gleicht dieses Problem auf ein Minimum aus. Aus jedem beobachteten Sensordatenwert können wir schließen, dass sich das getestete System in einem wohldefinierten Zustand befindet. Aufgrund der Messunsicherheit können jedoch einige der vorhergesagten Zustände wahrscheinlicher sein als andere innerhalb des Bereichs der Sensormesswerte. Zu diesem Zweck führen wir eine Unsicherheits-Kovarianzmatrix R_k ein, die sich aus dem von den Sensoren verursachten Rauschen ergibt, sowie einen Vektor der mittleren beobachteten Messwerte _k .
W ten sposób uzyskujemy dwa obszary rozmycia Gaussa – pierwszy wynikający z przewidywanego odczytu, a drugi z rzeczywistego odczytu z czujników.
Dzięki temu obszar poszukiwań optymalnego rozwiązania znacząco zawęża się i cały algorytm można wykonać od nowa w ten sam sposób, uzyskując jeszcze bardziej dokładne, tzn, jeszcze bardziej zgodne z rzeczywistością wyniki obliczeń na podstawie uzyskanych wcześniej danych pomiarowych.

Kalman-Verstärkung

Zur Bestimmung der Matrix, die die Kalman-Verstärkung definiert, muss eine eindimensionale Gauß-Kurve verwendet werden, wobei der 2i der Mittelwert zu berücksichtigen sind:

Multipliziert man die Gleichungen der Kurven, die die Normalverteilung für den vorhergesagten Zustand und den aus den von den Messsensoren abgelesenen Daten ermittelten tatsächlichen Zustand darstellen, miteinander, erhält man eine neue Gleichung der Kurve, deren Verteilung den Wertebereich für den gesuchten Zustandsvektor einengt:

Unter Verwendung der Matrix-Notation erhalten wir:

wobei K die Matrix ist, die die Kalman-Verstärkung definiert.

Endgültige Berechnungen

Wir erhalten zwei Verteilungen auf der Grundlage der Gaußschen Verteilung. Die erste ergibt sich aus der vorhergesagten Messung (9.1) und die zweite aus der beobachteten Messung.

Aus dem Gleichungssystem (9.3) bestimmen wir die Bedingungen, die den gemeinsamen Bereich der Verteilungen (9.1) und (9.2) definieren.

Je nach den Erfordernissen der Anwendung kann der gesamte Algorithmus mehrmals wiederholt werden, um noch genauere Ergebnisse zu erzielen.