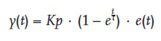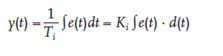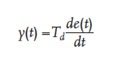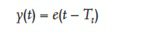Spis treści:
Automatische Regelungssysteme sind in modernen Automatisierungs- und Robotersystemen für Produktionsprozesse weit verbreitet. Ihr Zweck ist die Aufrechterhaltung bestimmter Parameter oder Werte im System, wie z.B. Temperatur, Druck oder Füllstand. Automatische Regelungssysteme arbeiten ohne menschliches Eingreifen, was Zeit und Ressourcen spart. Sie basieren in der Regel auf vorgegebenen Kontrollalgorithmen, die den Prozess optimal steuern. Der Autor wird sich auf die grundlegenden Komponenten automatischer Regelungssysteme konzentrieren, aus denen reale Regelungssysteme durch die Kombination ausgewählter Komponenten und die Auswahl ihrer Parameter entsprechend den Eigenschaften des betreffenden Regelungsobjekts aufgebaut werden.
Automatische Regulierung
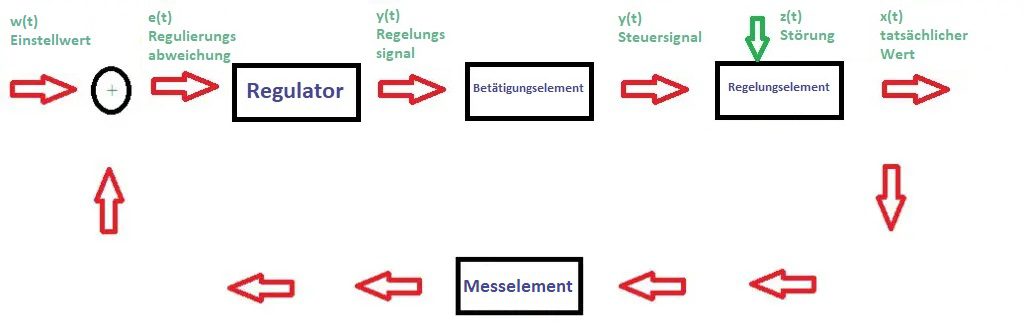
Die Aufgabe der Regelungstechnik ist es, die gewählten Werte der gesteuerten Größe zu erhalten. Sie besteht darin, das Regelungsobjekt so zu beeinflussen, dass der eingestellte Wert der gesteuerten Größe beibehalten wird oder dass ein bestimmter Charakter von Änderungen des Wertes dieser Größe gewährleistet wird. Das automatische Regelungssystem kann in offener Form oder als System mit Rückkopplung dargestellt werden, was bedeutet, dass die Information über die Differenz zwischen dem Sollwert der kontrollierten Größe und ihrem Istwert genutzt wird, um diese Differenz zu beseitigen.
In einem automatischen Regelungssystem wird der Wert der kontrollierten Größe x(t) mit einem geeigneten Messwandler gemessen. Daraus ergibt sich das Signal x'(t), das ein Maß für den Wert der Regelgröße ist. Die Regelabweichung e(t) wird dann als Differenz zwischen dem Sollwert der Regelgröße w(t) und ihrem Istwert berechnet: e(t) = w(t) – x'(t).
Unterteilung der automatischen Regelungssysteme
Automatische Regelungssysteme können unterteilt werden in:
- Konstanter Wert – es geht darum, einen konstanten Wert der kontrollierten Größe über die Zeit aufrechtzuerhalten, trotz Störungen, die auf das System einwirken,
- Tracking – die Essenz davon ist, dass der Controller mit dem Steuerobjekt so interagieren soll, dass sich die geregelte Größe auf eine vorgegebene Weise ändert.
Eine weitere Unterteilung der Regelungssysteme nach Art des Regelsignals ist:
- kontinuierlich (analog), wobei das Regelungssignal jeden Wert innerhalb eines bestimmten Bereichs annehmen kann,
- binär, wobei das Regelsignal einen von zwei möglichen Werten annehmen kann,
- diskret, wobei das Regelsignal einen der Werte annehmen kann, die zu einer endlichen Menge gehören.
Die Eigenschaften von automatischen Steuerungssystemen werden beschrieben mit Hilfe von:
- der Sprungantwort des Regelungssystems – dies ist eine grafische Darstellung seiner Reaktion auf eine Sprungaufforderung.
- Frequenzcharakteristik – eine grafische Darstellung der Reaktion des Reglers auf eine sinusförmige Anregung in Abhängigkeit von ihrer Frequenz. In der Regel werden zwei Frequenzkennlinien gezeichnet: Amplitudeals Diagramm der Abhängigkeit des Transmissionsmoduls des Controllers (Verhältnis der Amplitude des Signals am Eingang des Controllers zur Amplitude des Signals an seinem Ausgang) von der Frequenz des Eingangssignals, und Phaseals die Abhängigkeit des Transmissionsmoduls (die Phasenverschiebung zwischen dem Signal am Ausgang des Reglers und dem Signal an seinem Eingang) des Reglers von der Frequenz des Eingangssignals.
Komponenten von automatischen Regelungssystemen
In der Regel bestehen automatische Regelungssysteme aus den folgenden Komponenten:
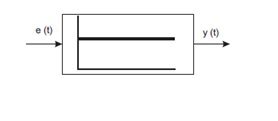
- proportional, der dadurch gekennzeichnet ist, dass das Signal an seinem Ausgang y(t) proportional zum Wert des Eingangssignals e(t) ist, das die Regelabweichung darstellt. Die Abhängigkeit des Ausgangssignals vom Eingangssignal ist wie folgt definiert:
y(t) = Kp-e(t)
Symbol
Erzwingung der Einheit
Sprungantwort auf unitäre Erzwingung
Informationen: Ein Proportionalglied ist ein trägheitsloses Glied. In der Realität reagiert jedoch jedes Proportionalglied auf eine Änderung des Eingangssignals mit einer gewissen Verzögerung. Ein ideales Proportionalglied zeichnet sich durch einen konstanten Wert des Proportionalitätskoeffizienten Kp aus, der unabhängig von der Frequenz der sinusförmigen Erregung ist, und durch das Fehlen einer Phasenverschiebung zwischen dem Signal am Ausgang des Reglers und dem Signal an seinem Eingang. Die Antwort des Proportionalglieds auf eine sinusförmige Erregung ist ein sinusförmiges Signal der gleichen Frequenz, das sich nur in der Amplitude unterscheidet.
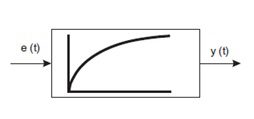
- Inertialsystem erster und zweiter Ordnung, das dadurch gekennzeichnet ist, dass das Signal an seinem Ausgang y(t) erst nach einer bestimmten Zeit proportional zum Antriebssignal e(t) ist. Die Abhängigkeit des Ausgangssignals von dem Eingangssignal ist wie folgt definiert:
Trägheitsglied erster Ordnung
Symbol
Erzwingung der Einheit
Sprungantwort auf unitäre Erregung
Informationen: Die Zeitkonstante des Trägheitsglieds erster Ordnung bestimmt die Trägheit des Reglers, d. h. wie schnell das Signal an seinem Ausgang beginnt, proportional zum Eingangssignal zu sein. In der Praxis wird davon ausgegangen, dass ein Trägheitsregler erster Ordnung nach einer Zeit, die drei Zeitkonstanten entspricht, zu einem Proportionalregler wird. Das Ausgangssignal nimmt dann einen Wert an, der etwa 95 % des Wertes von Kp e(t) entspricht. Die Antwort auf einen sinusförmigen Impuls ist ein sinusförmiges Signal mit derselben Frequenz, das sich in Amplitude und Anfangsphase vom Eingangssignal unterscheidet. Mit steigender Frequenz nimmt die Amplitude des Ausgangssignals ab, da das Ausgangssignal aufgrund der Trägheit nicht mit den schnellen Änderungen des Eingangssignals Schritt halten kann. Das Trägheitsglied erster Ordnung verhält sich wie ein Tiefpassfilter.
Symbol für Trägheitsintegralglied zweiter
- Ordnung – Abhängigkeit des Ausgangssignals vom Eingangssignal wie folgt definiert:
Symbol
Erzwingung der Einheit
Sprungantwort auf unitäre Erregung
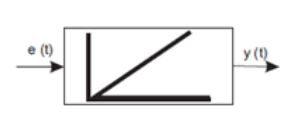
Information: Die Integrationszeitkonstante Ti ist die Zeit, nach der das Signal am Ausgang des Integralreglers den Sprungzwang erreicht. Das Antwortsignal ist ein linear ansteigendes Signal gemäß der Definition des Integrals. Mit der Zeit nimmt die Fläche unter dem Graphen der Funktion e(t) linear zu, so dass die Sprungantwort einem bestimmten Muster folgt. Die Anstiegsgeschwindigkeit des Ausgangssignals y(t) ist umgekehrt proportional zur Integrationszeitkonstante. Die Antwort des Integrationsglieds auf einen sinusförmigen Antrieb ist ein sinusförmiges Signal derselben Frequenz, wobei bei niedrigen Frequenzen des Eingangssignals die Amplitude des Ausgangssignals größer ist als die Amplitude des Eingangssignals, während die Amplitude des Ausgangssignals mit steigender Frequenz des Antriebs abnimmt. Ein Integralregler verhält sich wie ein Tiefpass-
- Differenzialfilter, der dadurch gekennzeichnet ist, dass das Signal an seinem Ausgang proportional zur Ableitung (Differenz) des Eingangssignals ist. Unter der Ableitung versteht man die Geschwindigkeit des Anstiegs oder des Abfalls des Signals und damit die Steilheit seiner Wellenform. Die Abhängigkeit des Ausgangssignals vom Eingangssignal ist wie folgt definiert:
Symbol
Erzwingung der Einheit
Sprungantwort auf unitäre Erregung
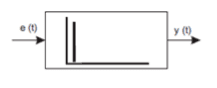
Information: Die Antwort des Differenzierglieds auf eine Stufenerregung ist ein Impuls, der zum Zeitpunkt der Stufenänderung der Erregung auftritt. Wäre das Eingangssignal perfekt gestuft, d. h. seine Anstiegszeit wäre gleich 0, würde am Ausgang eines idealen Differenzierglieds ein Impuls mit unendlich großer Amplitude und einer Dauer von Null erscheinen. Bei niedrigen Frequenzen des Eingangssignals ist die Amplitude des Ausgangssignals kleiner als die Amplitude des Eingangssignals, während die Amplitude des Signals am Ausgang mit zunehmender Impulsfrequenz zunimmt. Der Differenzialregler verhält sich wie ein Hochpassfilter.
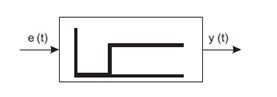
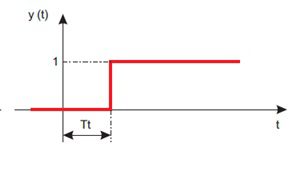
- Verzögerung – die Abhängigkeit des Ausgangssignals vom Eingangssignal ist also wie folgt definiert:
Symbol
Erzwingung der Einheit
Sprungantwort auf unitäre Erregung
Informationen: Die Reaktion eines Verzögerungsglieds auf eine Sprunganregung ist eine sprunghafte Änderung des Werts des Ausgangssignals, die mit einer bestimmten Verzögerung auftritt, während die Sprungwerte des Ausgangssignals und der Anregung gleich sind. Die Reaktion des Verzögerungsglieds auf eine sinusförmige Anregung ist ein sinusförmiges Signal mit der gleichen Frequenz und Amplitude, das jedoch gegenüber der Anregung verzögert ist.
Kombinierte Glieder von automatischen Kontrollsystemen
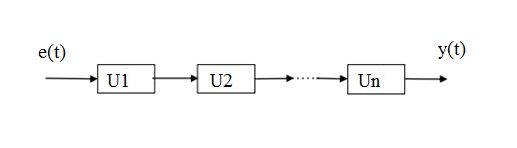
In realen Lösungen werden automatische Kontrollsysteme aus einigen ausgewählten Elementen aufgebaut. Die Elemente eines automatischen Kontrollsystems können in Reihe oder parallel geschaltet werden. Darüber hinaus ist es möglich, ein oder mehrere Elemente in eine Rückkopplungsschleife einzubinden.
- Reihenschaltung – das Signal vom Ausgang des vorherigen Glieds wird an den Eingang des nächsten Glieds angelegt (jedes Glied hat seine eigene Verstärkung Kp1, Kp2, usw.). Der Ersatzverstärkungswert Kp ist das Produkt aus den Verstärkungen der einzelnen Glieder.
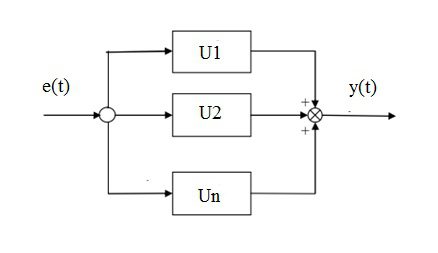
- Parallelschaltung – das Eingangssignal wird gleichzeitig an die Eingänge der einzelnen Glieder angelegt. Das Ausgangssignal eines Reglers, der aus mehreren parallel geschalteten Gliedern besteht (jedes Glied hat seine eigene Verstärkung Kp1, Kp2, usw.), ist die Summe der Ausgangssignale der einzelnen Glieder.
Basierend auf der Kombination der Glieder können verschiedene Arten von Reglern gebaut werden – proportional, proportional-differentiell, proportional-integral und proportional-differentiell-integral. Aufgrund der Komplexität der Beschreibung dieser Regler und nach Ansicht des Autors der Notwendigkeit, Fragen im Zusammenhang mit der Stabilität automatischer Kontrollsysteme und der Auswahl der Reglereinstellungen zu behandeln, werden diese Themen in einem anderen Beitrag behandelt.
