Inhaltsverzeichnis:
- 1 Boolesche Algebra in der Programmierung
- 2 Logische Funktoren
- 3 Logische Schaltungen
- 4 Nomenklatur der Zustände
- 5 Logikgatter in digitalen Schaltungen
- 6 George Boole
- 7 Boolesche Algebra – Grundsätze
- 8 Arten von Logikgattern
- 9 NOT-Gatter
- 10 AND-Gatter
- 11 NAND-Gatter (-AND)
- 12 OR-Gatter
- 13 NOR-Gatter
- 14 Das XOR-Gatter (oder EXOR-Gatter)
- 15 Logische Gesetze
- 16 Logikgatter – FAQ
Logische Gatter sind Werkzeuge, die die Bausteine von Maschinen, Automaten oder Robotern sind. Die Computer, die wir heute benutzen, verwenden Millionen von logischen Mechanismen, die als digitale Gatter (oder Logikgatter) bezeichnet werden. Dabei handelt es sich um elektronische Bauteile, die an ihren Eingängen binäre Signale empfangen und Werte von 1 oder 0 – wahr oder falsch – zurückgeben.
Logikgatter sind feste Komponenten in vielen Maschinen. Heutzutage handelt es sich meist um integrierte Schaltungen, die aus einer Reihe von entsprechend angeschlossenen Transistoren bestehen. Ein ähnlicher Effekt kann z. B. mit hydraulischen oder pneumatischen Vorrichtungen erzielt werden. Vereinfacht gesagt, besteht das Prinzip der Gatter darin, eine von zwei elektrischen Spannungen (Logikpegel) anzulegen. Dabei handelt es sich um eine Spannung mit Werten zwischen 0 V und 0,8 V (Pegel 0 – falsch), während der zweite Spannungswert zwischen 2 V und 5 V liegen sollte (Pegel 1 – wahr). Eine solche Unterscheidung – mit solchen Spannungswerten – wird in Schaltungen vom Typ TTL (Transistor-Transistor-Logic) verwendet.

Boolesche Algebra in der Programmierung
Boolesche Algebra ist eine Art algebraische Struktur – wenn Sie Programmierer sind und nicht direkt mit diesem Begriff vertraut waren, werden Sie wahrscheinlich schnell erraten, worum es sich handelt. Die Boolesche Algebra hat eine breite Palette von Anwendungen. Viele Programmiersprachen verwenden einen so genannten booleschen Typ (z. B. boolesche Variablen oder boolesche Funktionen, auch als logische Funktion bezeichnet) – Sprachen wie Pascal, C++, C#, PHP oder Java, um nur einige zu nennen. Eine boolesche Variable oder das Ergebnis einer booleschen Funktion kann nur einen von zwei Werten annehmen – 0 oder 1. Der boolesche Typ wird verwendet, um das Ergebnis einer Funktion zu bestimmen (wahr oder falsch) und um Ereignisse mit einem “Flag” zu kennzeichnen, und wird auch als Bedingung für eine bedingte Anweisung oder beispielsweise als Bedingung für das Verlassen oder Fortsetzen einer Schleife verwendet.
Logische Funktoren
Er wird auch als satzbildender Funktor bezeichnet und ist ein Ausdruck, der zusammen mit den Argumenten des Funktors, d. h. anderen Ausdrücken, eine Satzfunktion oder einen Satz bildet.
Boolesche Algebra – Formeln
[zdjęcie ukazujące wszystkie wzory Algebry Boole’a]
Logische Schaltungen
Sie werden auch als digitale Schaltungen bezeichnet. Sie arbeiten mit diskreten Werten. Sie werden auf der Grundlage von Logikgattern erstellt, die grundlegende logische Operationen wie Produkt, Negation oder Summe ausführen.
Nomenklatur der Zustände
Die Spannungspegel entsprechen direkt den logischen Werten der Booleschen Algebra. Ein logischer Pegel gleich Null wird oft mit dem Buchstaben F (von false, was “falsch” bedeutet) oder L (von low– was “niedrig” bedeutet) bezeichnet. Analog dazu wird ein Pegel gleich 1 oft mit dem Buchstaben T (von true – was “wahr” bedeutet) oder H (von high – was “hoch” bedeutet) bezeichnet.

Logikgatter in digitalen Schaltungen
Im Inneren des Computers finden ständig Operationen statt, bei denen der Computer lediglich logische Gatter verwendet – die Spannungspegel sind das Äquivalent zu Bits. Ein Logikgatter liefert an seinem Ausgang eine entsprechende elektrische Spannung, die wiederum in den oben definierten Bereich fällt und einen von zwei Zuständen anzeigt (1 – wahr oder 0 – falsch). Sie ergibt sich aus der logischen Funktion, die das Gatter ausführt (z. B. Konjunktion, Negation oder Alternative). Logikgatter, die in der Elektronik verwendet werden, sind Bauelemente, die mit entsprechend verbundenen elektronischen Bauteilen arbeiten – das sind vor allem Transistoren, Kondensatoren, Halbleiterdioden und Widerstände (Resistoren). Heutige Prozessoren bestehen aus Milliarden von sehr kleinen, geeignet verbundenen Transistoren. Sie sind der Schlüssel zum Betrieb jeder digitalen Schaltung. Jeder Transistor hat drei Elektroden – Source, Drain und Gate. Wenn an die letzte Elektrode eine Spannung angelegt wird, ändert sich die Leitfähigkeit des Kanals. Dieses Wissen über die Funktionsweise von Transistoren reicht aus, um zu verstehen, wie Logikgatter funktionieren. Logische Gatter können auch einfach als kleine schwarze Kästen betrachtet werden, an deren Eingang Spannungen angelegt werden, so dass am Ausgang eine von der Funktion (Eingangssignal) abhängige Spannung erscheint. Diese Art von Ansatz ist völlig ausreichend, um selbst die komplexesten digitalen Netzwerke zu entwerfen.
George Boole
Die Boolesche Algebra ist eine Art algebraischer Struktur, die nach dem bekannten Philosophen, Mathematiker und Logiker George Boole benannt ist. Aufgrund seiner Einführung des Konzepts der Booleschen Algebra gilt er als einer der Gründer der mathematischen Logik und der Computerwissenschaft. Er wurde am 2. November 1815 in Lincoln geboren und lebte bis zum Jahr 1859. Er wurde in eine Familie hineingeboren, in der sein Vater Schuhmacher war – dieser Vater wollte ihn auf eine gute Schule schicken, konnte dies aber mangels ausreichender finanzieller Mittel nicht tun. Er brachte seinem Sohn alles bei, was er konnte, und drängte ihn, Latein zu lernen, was damals eine Art Passierschein für die Oberschicht war. George lernte aus Büchern, und als Jugendlicher begann er, in Volksschulen zu unterrichten. Als er etwa 20 Jahre alt war, machte er sich mit den Werken von Joseph Lagrange und Pierre Laplace vertraut und begann, eigene Abhandlungen über Mathematik zu schreiben. Die ersten Arbeiten wurden schlecht redigiert, aber leider hatte George nicht die finanziellen Mittel, um seine Fähigkeiten an der Universität zu verbessern.
Dennoch wurde seine Arbeit so bekannt und wichtig, dass er 1844 mit der Medaille der Royal Society ausgezeichnet wurde. Später wurde er – trotz seiner fehlenden offiziellen Ausbildung als Professor an der Universität zugelassen. Im Jahr 1854 veröffentlichte er sein wichtigstes Werk mit dem Titel “An Investigation of the Laws of Thought, on which are founded the Mathematical Theories of Logic and Probabilities” (aus dem Englischen: “Eine Untersuchung der Denkgesetze, auf denen die mathematischen Theorien der Logik und der Wahrscheinlichkeitsrechnung beruhen“). Er trug direkt zum heutigen Stand der Digitaltechnik bei – der Betrieb von Millionen von Computern und Geräten auf der ganzen Welt funktioniert auf der Grundlage der Prinzipien der Booleschen Algebra.

Boolesche Algebra – Grundsätze
Die Boolesche Algebra definiert die folgenden grundlegenden Gesetze:
I – Gesetz der Abwechslung von Addition und Multiplikation. Bedeutet, dass das Ergebnis des Ausdrucks a x b gleich dem Ergebnis des Ausdrucks b x a ist (wobei das “x” das Multiplikationszeichen angibt). Ein Gleichheitszeichen kann zwischen die Ausdrücke a + b und b + a gesetzt werden.
II – Das Gesetz der Konnektivität der Multiplikation. Das bedeutet, dass das Ergebnis von a x b x c das gleiche ist wie das Ergebnis von a(b x c) und (a x b)c. Das gleiche Prinzip gilt für die Addition – das Gesetz der Konnektivität der Addition – das Ergebnis des Ausdrucks a+b+c ist gleich dem Ergebnis von (a+b)+c und a+(b+c)
III – Gesetz der Trennbarkeit von Multiplikation und Addition. Der Ausdruck a(b+c) ist gleichbedeutend mit dem Ausdruck (a × b)+(a × c). Das Gleiche gilt für die Addition im Verhältnis zur Multiplikation: Der Ausdruck a + b × c ist gleich (a+b)×(a+c).
Arten von Logikgattern
Die Funktionsweise von Logikgattern lässt sich mit Hilfe so genannter Wahrheitstabellen leicht aufschlüsseln. Diese beschreiben die aufeinanderfolgenden Kombinationen von Eingangszuständen und die entsprechenden Zustände am Ausgang des Gatters.
NOT-Gatter
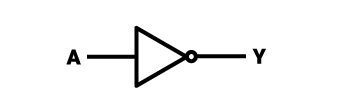
Das NOT-Gatter ist das einfachste der hier beschriebenen Gatter (und generell aller verwendeten Logikgatter). Seine Funktionsweise beruht auf der Negation (Umkehrung) des Signals, das es am Eingang erhält. In der Praxis sieht das folgendermaßen aus: Wenn ein Signal mit dem Wert 1 (wahr) am Eingang anliegt, wird ein Signal mit dem Wert 0 (falsch) am Ausgang ausgegeben. Umgekehrt wird bei einem Signal mit dem Wert 0 am Eingang eine 1 am Ausgang ausgegeben.
Beispiel 1:
Eingang = 1
Ausgang = 0
Beispiel 2:
Eingang = 0
Ausgang = 1
Das NOT-Gatter wird ebenfalls durch ein grafisches Symbol dargestellt – es handelt sich um ein gleichschenkliges Dreieck, das auch als nach rechts gerichteter Pfeil gesehen werden kann – an der Stelle, an der sich die längeren Schenkel schneiden, befindet sich ein Kreis, der seinen Scheitelpunkt tangiert (sein Durchmesser beträgt etwa ¼ der Länge der kürzeren Seite des Dreiecks). Der Eingang zum Gatter befindet sich links von der grafischen Darstellung (senkrecht zum kurzen Arm des Dreiecks), während der Ausgang rechts vom Symbol liegt (hinter dem umschriebenen Kreis). Das Gatter hat nur einen Eingang und einen Ausgang. Ein Beispiel für eine integrierte Schaltung (TTL), die 6 solcher Gatter (NOT) enthält, heißt “7404”.
AND-Gatter
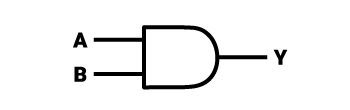
Bei der Funktion eines logischen AND-Gatters kann das Ergebnis 1 nur dann erzielt werden, wenn beide Eingänge gleich eins sind. Diese Art von Gatter gibt es mit drei oder vier Eingängen und mit noch viel mehr Eingängen. Beachten Sie, dass unabhängig davon, wie viele Eingänge im High-Zustand sind, ein High-Zustand am Ausgang nur möglich ist, wenn an jedem Eingang eine logische Eins anliegt.
Beispiel 1:
Eingang 1 = 1
Eingang 2 = 0
Eingang 3 = 1
Ausgang = 0
Beispiel 2:
Eingang 1 = 1
Eingang 2 = 1
Eingang 3 = 1
Ausgang = 1
Das logische Symbol eines AND-Gatters ähnelt einer Figur, die aus einem Quadrat und einem halben Kreis besteht (der entlang eines Durchmessers geschnitten ist, dessen Länge der Seite des Quadrats entspricht). Die rechte Seite des Quadrats ist mit dem flachen Teil des Halbkreises verbunden. Das Ganze ähnelt einem Pfeil mit einer geglätteten Pfeilspitze, die nach rechts zeigt. Auf der linken Seite des Quadrats befinden sich die Eingänge des Gatters und auf der rechten Seite der Ausgang, der dem Symbol des NOT-Gatters entspricht. Ein Beispiel für eine integrierte Schaltung (TTL), die 4 solcher Gatter (“AND-Gatter” mit zwei Eingängen) enthält, wird “7408” genannt.

NAND-Gatter (-AND)
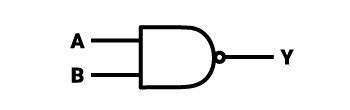
Die Funktionsweise eines NAND-Gatters (-AND) ist genau das Gegenteil eines AND-Gatters. Eine alternative Bezeichnung für NAND ist der Begriff “-AND”. – Der Bindestrich vor dem AND bedeutet Negation. So lässt sich auch die Funktionsweise eines NAND-Gatters interpretieren – es ist genau so, als würde man die entsprechenden Werte an den Eingang des UND-Gatters legen, das Ergebnis an dessen Ausgang erscheinen lassen und dann noch ein NICHT-Gatter durchlaufen. Man kann die NAND-Verknüpfung auch so interpretieren, als ob sich vor jedem Eingang des AND-Gatters ein NOT-Gatter befinden würde. Vereinfacht lässt sich die Funktionsweise eines NAND-Gatters wie folgt beschreiben: Ein niedriger Zustand (0) tritt nur auf, wenn an allen Eingängen ein hoher Zustand (1) auftritt. Es ist erwähnenswert, dass ein NAND-Gatter eine unbegrenzte Anzahl von Eingängen hat.
Beispiel 1:
Eingang 1 = 1
Eingang 2 = 0
Eingang 3 = 1
Ausgang = 1
Beispiel 2:
Eingang 1 = 1
Eingang 2 = 1
Eingang 3 = 1
Ausgang = 0
Das logische Symbol für ein NAND-Gatter ist fast dasselbe wie das Symbol für ein UND-Gatter. Es ist ein Quadrat, an dessen rechter Seite ein Halbkreis angehängt ist, der entlang des Durchmessers geschnitten ist und dessen Scheitelpunkte sich mit den Scheitelpunkten des Quadrats treffen. Das Ganze ähnelt einem Pfeil mit einer geglätteten Pfeilspitze, an deren Ende sich ein kleiner Kreis befindet, der etwa ¼ der Seitenlänge des Quadrats beträgt und dessen Durchmesser eine Verlängerung des Radius des Halbkreises ist und sich auf halber Höhe der gesamten Figur befindet. Der Kreis ist derselbe wie der für das NOT-Gatter beschriebene – er steht für die genaue Umkehrung des Symbols, neben dem er steht (das Dreieck ist das Symbol für die Summe – die Umkehrung ist die Negation, AND ist die Negation von NAND). Die Eingänge des Gatters befinden sich auf der linken Seite des Quadrats, während sich der Ausgang direkt hinter dem kleinen Kreis befindet. Ein Beispiel für einen integrierten Schaltkreis (TTL), der 4 solcher Gatter (NAND-Gatter mit zwei Eingängen) enthält, heißt “7400”, “7401” und “7403”.
OR-Gatter
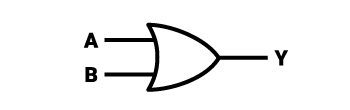
Am Ausgang eines OR-Gatters erscheint immer dann eine 1, wenn mindestens einer der Eingänge im High-Zustand ist. Das bedeutet auch, dass am Ausgang eine Eins erscheint, wenn mehr als ein Eingang einen hohen Wert hat. Die Null erscheint also nur dann am Ausgang, wenn alle Eingänge des Gatters ebenfalls auf Null gesetzt sind. Natürlich ist der Ausgang immer nur eine Eins. Ein typischer Schaltkreis hat zwei Eingänge, aber er kann auch unendlich viele Eingänge haben und funktioniert auf die gleiche Weise.
Beispiel 1:
Eingang 1 = 0
Eingang 2 = 1
Eingang 3 = 0
Ausgang = 1
Beispiel 2:
Eingang 1 = 1
Eingang 2 = 1
Eingang 3 = 1
Ausgang = 1
Beispiel 3:
Eingang 1 = 0
Eingang 2 = 0
Eingang 3 = 0
Ausgang = 0
Das logische Symbol für das OR-Gatter ähnelt wiederum einem Pfeil. Die Ähnlichkeit mit dem Symbol für das AND- und NAND-Gatter ist unübersehbar, aber es ist einfacher, es von Grund auf zu beschreiben. Das Symbol des OR-Gatters kann als eine Figur beschrieben werden, die aus einem zusammenhängenden Quadrat und einem gleichschenkligen Dreieck besteht, dessen kürzeste Seitenlänge gleich der Höhe der Seite des Quadrats ist, an dessen rechte Seite das betreffende Dreieck angrenzt. Die linke Seite des Quadrats ist ausgeschnitten, und der Raum nach dem Ausschnitt hat die Form eines Bogens, der ein Fragment eines tangentialen Kreises ist, dessen Durchmesser um ein Vielfaches größer ist als die Seite des Quadrats. Die beiden Arme des angefügten gleichschenkligen Dreiecks sind nach außen gewölbt, wodurch das Ganze stromlinienförmiger wird, während das scharfe Ende des “Pfeils” erhalten bleibt. Die Konvexität kann so definiert werden, dass die sich berührenden gleichen Seiten des Dreiecks zwei Kreisabschnitte sind, deren Durchmesser um ein Vielfaches größer ist als jede Seite des Dreiecks. Ein Beispiel für eine integrierte Schaltung (TTL), die 4 solcher Gatter enthält, heißt “7432”.
NOR-Gatter
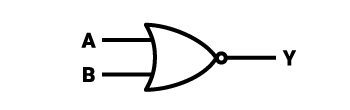
Analog zu den oben gezeigten Gattern kann man erraten, für welche Art von Operation das NOR-Gatter steht. Wenn man sich die vorherigen Namen ansieht, kann man eine Tendenz feststellen: Gatter, deren Namen der Buchstabe N vorangestellt ist, funktionieren genau umgekehrt wie ihr Original. Das liegt daran, dass der Buchstabe N (von not, was “nicht” bedeutet) für die Negation steht (wie bei AND und NAND). Die Funktionsweise eines NOR-Gatters kann als die komplette Umkehrung der Funktionsweise eines OR-Gatters beschrieben werden – man kann es so betrachten, dass es nacheinander als OR-Gatter auf alle Eingangssignale einwirkt, die es erhalten hat, und dann sein Ausgangssignal in den Eingang eines NOT-Gatters legt – das Ergebnis zeigt an, dass das NOR-Gatter in Betrieb ist. Natürlich kann man auch davon ausgehen, dass vor jedem Eingang des OR-Gatters ein NOT-Gatter angelegt wird – in diesem Fall stammt jeder Eingang des OR-Gatters vom Ausgang der NOT-Gatter. Um die Beschreibung des Funktionsprinzips zu vereinfachen, gibt ein NOR-Gatter an seinem Ausgang immer einen niedrigen Zustand zurück, es sei denn, alle Zustände sind auf 0 gesetzt. Solche Gatter können eine unendliche Anzahl von Eingängen haben.
Beispiel 1:
Eingang 1 = 1
Eingang 2 = 0
Eingang 3 = 1
Ausgang = 0
Beispiel 2:
Eingang 1 = 0
Eingang 2 = 0
Eingang 3 = 0
Ausgang = 1
Beispiel 3:
Eingang 1 = 1
Eingang 2 = 0
Eingang 3 = 0
Ausgang = 0
Das grafische Symbol für ein solches logisches Gatter ist wiederum analog zu den Veränderungen im Erscheinungsbild, die zwischen logischen Gattersymbolen und logischen Gattersymbolen, die die Umkehrung der ersteren waren, auftraten. Der Prototyp der negierten Version des Symbols behält am rechten Ende einen kleinen Kreis bei, dessen Durchmesser in etwa ¼ der Höhe der gesamten Grafik entspricht. In diesem Fall handelt es sich um das zuvor beschriebene Quadrat, dessen linke Seite leicht eingerückt ist – die Form der Einrückung sieht aus wie ein kleiner Kreisausschnitt, der ein Mehrfaches des Durchmessers der Seite des Quadrats beträgt. Die rechte Seite des Quadrats grenzt an ein gleichschenkliges Dreieck, dessen Seiten abgerundet sind – leicht überlagert von einem Kreisausschnitt mit sehr großem Durchmesser. Neben dem spitzen Ende auf der rechten Seite befindet sich ein kleiner Kreis – ein grafisches Zeichen für die Negation. Auf der linken Seite befinden sich die Eingänge des logischen Gatters (auf der ausgeschnittenen Seite des Quadrats), und hinter dem kleinen Kreis befindet sich der Ausgang des Gatters. Das Ganze sieht aus wie eine Art Gewehrkugel. Ein Beispiel für eine integrierte Schaltung (TTL), die 4 solcher Gatter enthält, heißt “7402”.
Das XOR-Gatter (oder EXOR-Gatter)
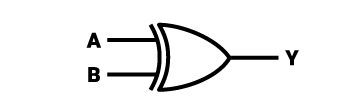
Das EXOR-Gatter (“Exclusive-OR”, d. h. “ausschließlich nicht”) ist eine der einzigartigen Funktionen, die nicht mehr zur Gruppe der gebräuchlichsten – grundlegenden Logikgatterfunktionen gehört. Es ist ein Gatter, das immer genau zwei Variablen an seinem Eingang hat (es ist eine Funktion von zwei Variablen). Es erhält immer dann einen hohen Zustand, wenn nur einer der Eingangszustände gleich einer logischen Eins ist. Ein Low-Zustand am Ausgang tritt auf, wenn beide Eingangswerte gleich sind. Das XOR-Gatter führt eine modulo-2-bitweise Additionsoperation durch.
Beispiel 1:
Eingang 1 = 1
Eingang 2 = 1
Ausgang = 0
Beispiel 2:
Eingang 1 = 0
Eingang 2 = 0
Ausgang = 0
Beispiel 3:
Eingang 1 = 1
Eingang 2 = 0
Ausgang = 1
Beispiel 4:
Eingang 1 = 0
Eingang 2 = 1
Ausgang = 1
Die grafische Darstellung eines XOR-Logikgatters ist ein Symbol, das ähnlich aussieht wie die grafische Darstellung eines OR-Logikgatters. Das XOR -Gatter sieht vereinfacht wie eine Kugel aus, hat aber zusätzlich eine Linie parallel zur linken Seite des Symbols. Die linke Seite des Symbols ist die ehemalige Wand eines Quadrats, die durch den Ausschnitt in Form einer Kreisscheibe mit sehr großem Radius konkav ist. Die zuvor beschriebene parallele Linie, die sich links vom Symbol befindet, hat die Form einer Kreisscheibe mit dem gleichen Radius wie der Radius des Kreises, dessen Scheibe aus der linken Seite des Quadrats ausgeschnitten wurde.
Logische Gesetze
Dies sind Sätze, die bei jeder Interpretation der in ihnen enthaltenen außerlogischen Konstanten wahr sind. Eine logische Summe ist ein logischer Satz, auch Alternative genannt, der Form p oder q.
Logikgatter – FAQ
Wie hilfreich war dieser Beitrag?
Klicke auf die Sterne um zu bewerten!
Durchschnittliche Bewertung 4.7 / 5. Stimmenzahl: 42
Bisher keine Bewertungen! Sei der Erste, der diesen Beitrag bewertet.



















